Normal Surfaces

Normal Surfaces - Definition

We begin this visualization process with a discussion of normal surfaces only. Recall our definition of the six principal projection planes: Front, Back, Top, Bottom, Left, Right. A normal surface is a surface that is perpendicular to two of the principal planes and parallel to the third. To illustrate the simplest example of normal surfaces, we will use a rectangular block. 

The following site is a fairly comprehensive study of the "Normal surface".  Most of the images shown below are excerpts from this site.  The site is actually quite good and I encourage you to view it thoroughly after a brief review of the images/definitions below.

Normal Surfaces in Orthographic Projection site

The key phrase for this lesson - as well as the companion lessons on inclined, oblique and cylindrical surfaces -- IS VISUALIZE.

Visualization Process

The ability to form a mental picture of an object from a drawing is not acquired all at once; it must be accomplished gradually. As with the study of any language for communication, we must first learn the simple words and phrases. So in visualizing an object we must start with lines and plane surfaces on simple objects before we progress to more complex objects.

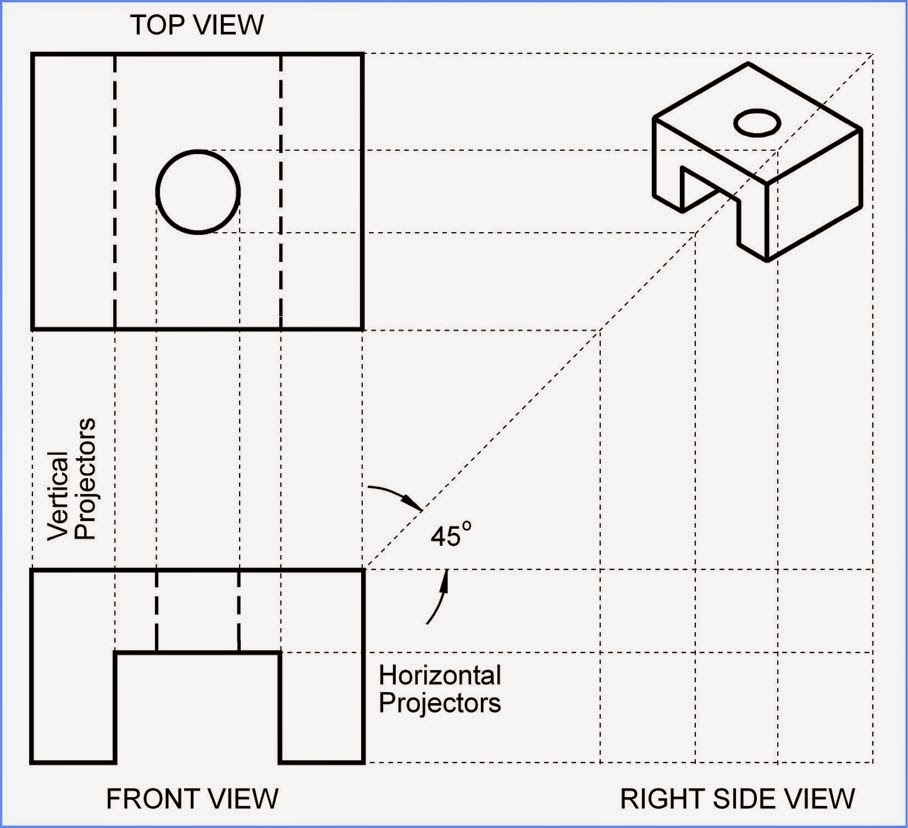
You must develop the ability to "read" each feature of the object by interpreting the information given within the drawing. This ability will help you to visualize the shape of objects. Rather than staring at orthographic views in an attempt to visualize the object, consider the technique of reading the lines and areas. Each area can represent a surface, while each line on the object can represent either the line view of a surface, or the edge intersection of two surfaces.

Normal Surfaces - Definition

Visual example of a Normal Surface

We begin this visualization process with a discussion of normal surfaces only. Recall our definition of the six principal projection planes: Front, Back, Top, Bottom, Left, Right. A normal surface is a surface that is perpendicular to two of the principal planes and parallel to the third. To illustrate the simplest example of normal surfaces, we will use a rectangular block. 

Now what this means in respect to the figure below is that the top surface is NORMAL to the "front" view and the "right" view while the top surface is parallel to the "top surface plane".

The image below left is an isometric view while the image below right is an orthographic view.

                                                         

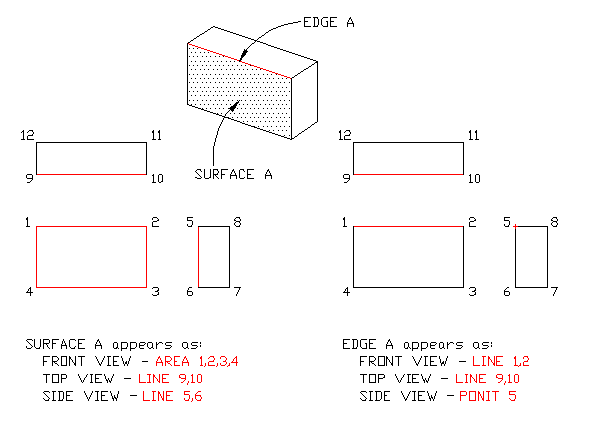
In Example N-1 below, surface A and edge A are identified in the isometric (3D pictorial) view. Identify the same surface and the same edge in each of the three orthographic views (front, top, and side) provided. 

Surface A is shown "True size" because surface A is parallel with the "frontal surface plane", while surface A is also perpendicular to the other two "surface planes" - in this case the top surface plane and the right surface plane.  The result is that surface A is normal (at a 90 degree angle) to the top and the right side surface planes.  This is "pictured" for us as surface A and is True sized while the top and right views of "surface A" are simply LINES both of which are also true sized.

 Now look at the solution of the same surface and the same edge. 

 

Notice that the surface A appears as an area in the front orthographic view. Surface A is parallel to the frontal projection plane, and therefore it appears true size (TS) in that view. 

Surface A is perpendicular to both the horizontal and profile projection planes, and therefore appears as a line in those views.

Now you may have a tendency to "get confused" by the terms "frontal, horizontal and profile" projection planes.  The frontal projection plane simply refers to "the surface plane" upon which the front view lies completely flat (this is the meaning of "parallel" with this plane)

The horizontal projection plane refers to the horizontal plane that is perpendicular to the frontal projection plane (the top view) and the profile projection plane (right view) refers to the OTHER projection plane that is perpendicular to the frontal projection plane.  

This other plane is a vertical plane that is perpendicular to the frontal projection view while the previous perpendicular plane was in the horizontal direction.
 

Edge A appears as a line in the front and top views. (Edge A is actually the intersection of the frontal and horizontal projection planes in respect to the boundaries of the object).  

Edge A is parallel to the frontal and horizontal projection planes and therefore appears true length (TL) in those orthographic views. Edge A is perpendicular to the profile plane and therefore appears as a point in that orthographic view. 

Lab exercise:  Using a standard sized sheet of paper sketch an isometric view of a rectangular block as shown in example N-1.

1)  Shade surface A and number the four corners of surface A (1,2,3,4) as shown in red above.  Put these numbers in the proper corners of the isometric view that you have drawn.

2)  Add numbers 5 and 6 to the proper "place" next to numbers you have labeled as the corners of surface A on the isometric view.

3)  Add numbers 9 and 10 to the isometric view in the same manner as step 2.

Answers to Lab exercise:  The upper left corner should be labeled (9,1).  The upper right corner should be labeled (2,10,5).  The lower left corner should be labeled (4 only). and the lower right corner should be labeled (3.6).

Now to turn in for a grade, I want you to repeat this procedure with Surface B as shown in example N-2.

1) Letter your name, section number and seat number in the upper right hand corner of your paper.

2) Using a pencil, provide an isometric sketch of the rectangular block shown in example N-2.

3) On the isometric view that you have sketched, label each corner of surface B using the numbering system shown in this example.

For the following - place the numbers in the proper location (just like the practice problem above)

        a) show the corners 9,10,11,12

        b) show the line (1,2)

        c) show the line (5,8)

Another example: N-2

In Example N-2, surface B and edge B are identified in the isometric (3D pictorial) view. Identify the same surface and the same edge in each of the three orthographic views (front, top, and side) provided. 

 

 Notice that the surface B appears as an area in the top orthographic view. Surface B is parallel to the horizontal projection plane, and therefore it appears true size (TS) in the top view. Surface B is perpendicular to both the frontal and profile projection planes, and therefore appears as a line in those views.
Edge B appears as a line in the top and side views. Edge B is parallel to the horizontal and profile projection planes and therefore appears true length (TL) in those orthographic views. Edge B is perpendicular to the frontal plane and therefore appears as a point in that orthographic view.

 

In Example N-3, surface C and edge C are identified in the isometric (3D pictorial) view. Identify the same surface and the same edge in each of the three orthographic views (front, top, and side) provided.

  Notice that the surface C appears as an area in the profile (right-side) orthographic view. Surface C is parallel to the profile projection plane, and therefore it appears true size (TS) in the profile view. Surface C is perpendicular to both the horizontal and frontal projection planes, and therefore appears as a line in those views.
Edge C appears as a line in the front and side views. Edge C is parallel to the frontal and profile projection planes and therefore appears true length (TL) in those orthographic views. Edge A is perpendicular to the horizontal plane and therefore appears as a point in that orthographic view.

 Normal Surfaces in Orthographic Projection

 In the previous examples (N-1 through N-3), the normal surfaces that were identified were all simple rectangular shapes. It is important to realize that rules for normal surfaces apply regardless of the shape of the surface. A normal surface of any shape will always appear as a line in two of the principal views. It will always appear true size in the third view.

Surface A

Surface B

Surface C 

To help us reinforce the concept that A normal surface of any shape will always appear as a line in two of the principal views. It will always appear true size in the third view, I want us to look at the Lego pictures. 

frontal view

Top View

Profile or right view

The point here is that while looking at the frontal view - the right (profile) view as well as the top view BOTH appear as only a line.

If we switch over and look look at the profile view - the same is true regarding both the top and the front views.

Switching to the top view - we can see that the front and the right side are both portrayed as only lines.

The images below will serve as an introduction to the next lesson (Inclined surfaces)

The remaining images can be viewed more completely (as well as other available features) on the link provided at the beginning of this post.  They are provided below for your convenience as a quick review.

 Normal surfaces in Orthographic Projections 

Example N-5

  In cases where the top and front views are given, a good starting point is to identify those features which are visible in the front and top views of the object, find the feature in the other given view and then create their representations in the missing side view. Assume that visible bounded areas represent normal surfaces.

 The top of the object appears as a line (27,30) in the front view. The top appears as an area (11,10,9,8,7,6,20,21,22,23,24,25) in the top view. Projection of that surface into the side view gives a horizontal line (A,B).

 (Next think about the front surface(s) of the object.)

 The front of the object appears as lines (24,25) and (21,20) in the top view. There are two separate surfaces on the front. These two surfaces appear as areas (27,28,43,42) and (29,30,31,44) in the front view. Projection of those surfaces into the side view gives a vertical line (A,C)

 (Next look at the remaining visible areas in the front view, starting with (28,29,44,43))

 Area (28,29,44,43) is a visible TS area in the front view. Line (23,22) is the representation of that surface in the top view. Projection into the side view gives line (A,B), a hidden line.

(Next look at area (42,31,34,35,36,37,38,39))

 Area (42,31,34,35,36,37,38,39) is a visible TS area in the front view. Line (26,19) is the line view of that surface. Projection into the side view gives line (A,B).

(Next look at areas (41,42,39,40) and (31,32,33,34))

 (31,32,33,34) is a visible area in the front view. (6,5) is the line view of that surface in the top view. (29,30,31,44) is a visible area in the front view. (7,6) is the line view of that surface in the top view. Projection of these two surfaces into the side view gives line (A,B). Because of symmetry, areas (27,28,43,42) and (41,42,39,40) could be treated the same way. When projected into the right side vioew these surfaces would appear as a hidden line (A,B) but due to the precedence of object lines, nothing else is added to the side view.

(Next look at area (37,36,35,38))

 The area (37,36,35,38) by orthographic reading COULD be represented by line (18,17) or line (13,14). Since we have already identified surface (42,31,34,35,36,37,38,39) as line (26,19), surface (37,36,35,38) cannot be (18,17). Surface (37,36,35,38) appears a line (13,14) in the top view. Draw line (A,B) in the side view. Consider the visibility of that line. 

(Next look at remaining visible areas in the top view, starting with (3,4,5,7) and (1,2,10,12))

 (3,4,5,7) appears as a TS area in the top view. It appears as edge (44,32) in the front. Projection gives line (A,B) in the side view. Due to symmetry, this also accounts for surface (1,2,10,12). Recognize that line 43,44 has not been accounted for. There is another surface on the same height as the two shaded areas above. We will remember this later.

(Next look at area (15,16,8,9)

Video Exercise 1-6 Orthographic Projection

By way of review - I want to go over some things to help alleviate some common errors that I am seeing in your work.

1) use of projectors to properly align the views presented - notice the image below:

 In this figure notice how there is a correlation between the "visible" vertical lines and the vertical projection lines.  For every visible vertical line there is a corresponding vertical projection line.  The same is true for the "visible" horizontal lines and the horizontal projection line.

The PURPOSE of the projection lines  is A) to establish the proper width of the next view.  Notice how the width of the top view is the EXACT width of the front view.  This is ensured by drawing the width of the top view completely WITHIN the two most extreme vertical projection lines.  An additional purpose of the left and right most vertical projection lines is to proper align the top view with respect to the front view.  The remaining interior vertical projection lines ensure the proper location on the top of the features indicated at their origin on the front view.

This same practice is duplicated regarding the horizontal lines.  Notice the "upper most" and "lower most" horizontal projection lines.  There purpose is A) to ensure that the height of the right side view does not exceed the height of the front view.  The additional purpose B) is to align the height of the right side view WITHIN the horizontal projection lines originating with the front view.  C) The remaining projection line properly locates the top of the milled feature that is evident in the front view.

The projection line at the 45 degree angle is required in order to properly locate BOTH the top and right side views with respect to each other AND with respect to the front view.  You will notice that there is a 1 to 1 correlation between the projectors that intersect the angled projector and the horizontal "visible lines" in the top view.  (note the upper and lower part of the hole).  The extreme points of this hole are treated as though they were a "visible" horizontal line for the purpose of proper alignment/location of that feature.

Another common mistake is the orientation of the views when an orthographic projection drawing is created.  Notice the image below:  It is imperative that you familiarize yourself with the skill of visualizing the different views based upon the "front view".

The six views that are possible on any orthographic projection should ALWAYS be drawn in the arrangement and/or order shown below.  You can be 100% certain that you WILL BE tested on this concept.

 
 

 Be sure to remember the Glass Box Method - it will help you visualize in the absence of being able to use a physical object to create an orthographic projection drawing.

On the image shown below, use standard orthographic techniques to draw the three principle views of the image.  You can copy and paste this image onto a word document to have a paper copy on which to work or simply use graph paper of your own.  The answer (correct images) will be shown later in this same post.  Try it on your own first.

This is a second practice image.  Do for this image as you did for the first image above.  Again the solution will be shown later in this post, but try it on your own first.

The following is exercise 1-8 in your text book.  Complete this worksheet.  Once again, this is a practice exercise and the answer will be given at the end of this post.

Note for Section 002 - A test has been scheduled for the next meeting time.  The text will consist of questions on the power point slides we have been reviewing AND there will be a drawing component on the test as well.  You will be required to draw in a similar manner to the way that we have been practicing in our past lessons.

Answers to Video exercise 1-6  The audio is not good on this one, but I have solved the problem and it is really good on latter lessons.

https://www.youtube.com/watch?v=L60HdAo7PDM&feature=youtu.be&hd=1

Answers to Video Exercise 1-7  Click below to see the answers to exercise #7.

Answer to Video Exercise 1-7 

Answers to Exercise 1-8 above:

Post any comments you have about the lesson.  Give me some constructive feed-back.  My goal is to make each lesson as engaging and as informative as possible.  Let me know if I hit the mark on this one.

Lego Exercise A

Lego Exercise.  Whole class Orthographic projection.

Provide (on graph paper) ALL six of the orthographic views of this object.  Ignore the circular tabs.

Make your first attempt by viewing ONLY the isometric view above.  As the front view choose the short end of the blue piece as it protrudes toward you and is located on the right with the yellow block located on the left.  Name this "attempt ONE".  After completion of "attempt ONE" check your work by viewing the images below.

Choose this as the FRONT view then properly label the remainder.

 

 

 

 

 

 

After this activity we will practice on the following object.  After viewing the object below, provide the THREE typical orthographic views.  Do your work on graph paper and be sure to letter your name, section and seat number in the upper right hand corner of your paper.

The answer to this is given below, but try to solve the problem BEFORE looking at the solution.





Your homework assignment will be the following problems.  They are found in your text book on pages 55, 57 and 59.  Do the work on the paper provided in your book.  Be sure to letter your name, section number and seat number as this will be part of your assignment.



Answer to P1-4 in class practice

 Homework problems listed below:

 Remember during our next scheduled class, we will have a test over the material on the slides and you will be given an object to draw similar to the exercises we have practicing in class.

Lettering, Sketching and Orthographic Projection

What is Engineering Graphics?  A set of rules and guidelines that help you create an Engineering Drawing.

   

What is an Engineering Drawing?   A drawing that communicates an idea or design.

 

Examples of Engineering Drawings

→Mechanical Engineers (factory/manufactured parts)

•Detailed drawing of a part that needs to be machined.

→Electrical Engineers (appliances to power transmission)

•A circuit schematic.

•Circuit board layout. (electronics)

→Civil Engineers (topography/landscapes)

•Plans for a bridge.

•Road layout.

ØWhat will we learn in Chapter 1?

→How to create an orthographic projection.

Key points

→An orthographic projection is a 2-D representation of a 3-D object.

→A system of drawings that represent different sides of an object.

→Project edges perpendicular to planes of projection

→Represent a shape using 2 or more views

→Gives enough information to manufacture the part.

Orthographic projection  = 2-D representation of a 3-D object. 

Isometric view            Orthographic view

 

An orthographic projection represents different sides of an object.

 

 

The Six Principal Views

The 6 principal views are created by looking at the object, straight on, in the directions indicated.

 

How do we create the 6 principal views?

Consider a pair of dice – each number is a view.  Choose one number for the front and then determine the remaining five views. 

The object is placed in a glass box.

The sides of the box represent the 6 principal planes.

 Left, Front, Right, Rear, Top, Bottom

 

 

The image of the object is projected on the sides of the box.

VISUALIZE !!!